|
|
Loi Ngyen and Tu Tran
students at The University of North Florida
Consider the following conjecture:
Let MN and PQ be two perpendicular diameters in a circle with center O, and A, B be two points on MO and ON such that MA=OB. If line BQ intersects the circle at C, then the angle CAQ is a right angle.
In this note we prove that the measurement of the angle CAQ is between
88.21 and 90 degrees, the conjecture is not true although it looks like
true very much.
Integral Functions Whose Right Derivatives
are Average Values of Periodic Functions
Paul Fishback, Nicholas Ceglarek (student), and Tobias Moleski (student)
Grand Valley State University
The First Fundamental Theorem of Calculus asserts that if f is
continuous on the unit interval [0,1], then the integral function 
is
right-differentiable at the origin. An interesting class of highly-oscillatory
functions that does not satisfy this theorem’s hypothesis consists of functions
where g is continuous and periodic. We show that for any member
of this class, the corresponding integral function is in fact right-differentiable
at the origin, and the value of the right derivative there equals the average
value of g over one period. We also construct a counterexample showing
how this result does not hold true in general when one replaces g
by an arbitrary bounded, continuous function.
On Jacobians in Multiple Integrals
Prem N. Bajaj
Wichita State University
The paper draws attention to the sign of the Jacobian, J, of transformation
for multiple integrals. an example is provided where the Jacobian takes
both positive and negative signs on the region of integration, and consequently,
requiring the integration to be evaluated separately on the regions where
the Jacobian takes positive and negative signs.
An Approximation to the Logarithmic Integral
Paul S. Bruckman
This paper gives an explicit approximation to the logarithmic integral
function li(x), astonishingly accurate within the range of values
explored. The comparison between the true values of li(x) and the
approximation formula is made for x=10^m, m=3,4,…,18. It
is well-known, of course, that if li(x) is itself a reasonable good
approximation to the prime counting function . The approximation formula
itself, denoted by f(x), is expressed as x times a polynomial
in 1/log(x).
On the Chromatic Number of the Middle Graph of a Graph
Masakazu Nihei
Fujishiro High School
Fujishiro, Ibaraki, 300-1537, Japan
Let G be a graph, let A be the vertex chromatic number of G,
and let B be the maximum degree among the vertices of G. The middle
graph M(G) of a graph G is the graph obtained from G
by inserting a new vertex into every edge of G and by joining by
edges those pairs of these new vertices which lie on adjacent edges of
G.
Involutions in Permutations
Subhash C. Saxena
Coastal Carolina University
In Geometry, an involution or involutory transformation is a transformation
which is its own inverse, and is not the identity. Its period is two. In
Abstract Algebra textbooks, this term is not commonly discussed in the
context of permutations. In this paper, we examine and explore involutory
permutations. Such involutions form building blocks of permutations,
in
the same manner as line reflections on a plane are building blocks of all
Euclidean transformations. A recursive relation is developed and two theorems
are proved.
Geometric Interpretations of the Continuous Mean
Arvind Shah and Xin-Min Zhang
University of South Alabama
In this paper, we provide some geometric interpretations for the continuous
mean. In particular, for a given family of simple closed plane curves,
we discuss the relationship between the average value of their areas and
the average value of their isoperimetric quotients.
A note on ‘Analytical Formulas for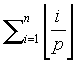 
’
Hans J. H. Tuenter
York University
This note gives a simple derivation of the analytical formulas for the
sums 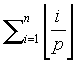where
p is an arbitrary positive integer.
What is a Proof?
Clayton W. Dodge
University of Maine
Much of our mathematics is taught by rote, with the result that many
students have little feeling for the unity and structure of the subject.
Even young children, however, can understand and appreciate this structure
through proofs, if those proofs are presented at an appropriate level.
Some examples are presented in this paper.
Scheduling Round-Robin Tournaments
James Oehmann (student)
University of North Florida
To schedule round-robin tournaments means to arrange N different
teams, so that each team plays every other team exactly once. A method
of filling numbers in a table is established, which is incredibly simple
and quick. No preliminary mathematics knowledge is needed.
Math his passion, teaching his life . . .
Donald E. Miller and Laura Meyers (student)
Saint Mary’s College
Milko Jeglic, a college faculty member and superintendent of Slovenian primary schools before WWII, was forced to flee his native land during the communist overthrow of its government. After spending five years in the refugee camps of Austria, he found his way to Saint Mary’s College in Notre Dame, Indiana. there, he distinguished himself while serving as a member of its Mathematics Department for almost three decades. Following his death in December 1997, professional recognition came for Jeglic with posthumous induction into the Indiana Epsilon Chapter. His story is an inspiration to aspiring mathematicians.
